深入思考FairMOT及其变体

创新点1：Conflict-Aware Multi-Task Optimization for Object Tracking

该领域前沿进展，blog推荐

$$\mathbb{E}_{x,y\sim\mathcal{D}_T}[\ell(h_T(x),y)]\leq\hat{\mathcal{L}}_T+\mathcal{R}_T(H_T)+\mathcal{O}\left(\sqrt{\frac{\log(1/\delta)}{n_T}}\right)$$

$\hat{\mathcal{L}}_T$ 是经验损失；

ℛ_T(H_T) 是假设空间 H_T 的 Rademacher 复杂度。

设 m 个任务，平均每个任务有 n 个样本，H 是共享表示的函数类：

$$\mathbb{E}_T\left[\mathbb{E}_{x,y\sim\mathcal{D}_T}[\ell(h_T(x),y)]\right]\leq\frac{1}{m}\sum_{i=1}^m\hat{\mathcal{L}}_{T_i}+\mathcal{O}\left(\frac{C(H)}{\sqrt{mn}}\right)$$

相比单任务的 $\mathcal{O}(1/\sqrt{n})$，MTL 将样本数放大为 mn。

从多任务学习框架，我们可以得知，多任务学习（MTL）通过共享表示来提高学习效率，然而这一假设的前提是，任务关联性越大越好。即式子中C(H)不可以太大！如果两个任务的共性过低，共享表示会导致性能显著下降。（例如你给一个人布置俩任务，又让他当模特保持身材，又让他比赛相扑增加体重，可想而知这个人的学习必然是不顺利的）,在数学上我们可以得出如下的推论

$$C(H) \downarrow \rightarrow \cos\theta=\frac{\langle\nabla_{\theta_s}\mathcal{L}_{\det},\nabla_{\theta_s}\mathcal{L}_{\mathrm{reid}}\rangle}{\|\nabla_{\theta_s}\mathcal{L}_{\det}\|\cdot\|\nabla_{\theta_s}\mathcal{L}_{\mathrm{reid}}\|}\approx1$$

出于这一理论，我们可以设计一个梯度门控模块

f_det 为 anchor-free heatmap 分支；

f_reid 为 linear embedding + triplet loss；

两个任务共享 θ_s，目标是构造一个在联合分布 𝒟_joint 上最优的 ϕ(x; θ_s)与最优的优化策略。

通过动态调节特征通路，理论上可以保证任务损失方向一致性，即

𝔼_x[cos (∇_θsℒ_det, ∇_θsℒ_reid)] > 0

其中，冲突计算模块实时计算夹角（极低时间复杂度，可以忽略不计） $$\theta(x)=\arccos\left(\frac{\langle\nabla_{\theta_s}\mathcal{L}_{\det}(x),\nabla_{\theta_s}\mathcal{L}_{\mathrm{reid}}(x)\rangle}{\|\cdot\|\|\cdot\|}\right)$$

自适应特征解耦模块（Adaptive Feature Routing）引入门控设置：

ϕ_det(x) = G(θ(x)) ⋅ ϕ(x),  ϕ_reid(x) = (1 − G(θ(x))) ⋅ ϕ(x)

其中 G(θ) 是一个门控函数，例如： $$G(\theta)=\frac{1}{1+\exp(-\alpha(\theta-\beta))}$$ 或者 G(θ) = σ(a ⋅ (θ − π/4)) 当梯度方向相近（θ 小）→ 更多共享；

冲突时（θ 大）→ 更多解耦。

也就是损失函数保持不变，但共享特征使用带门控的 ϕ_det, ϕ_reid 进行学习。

20250707104115

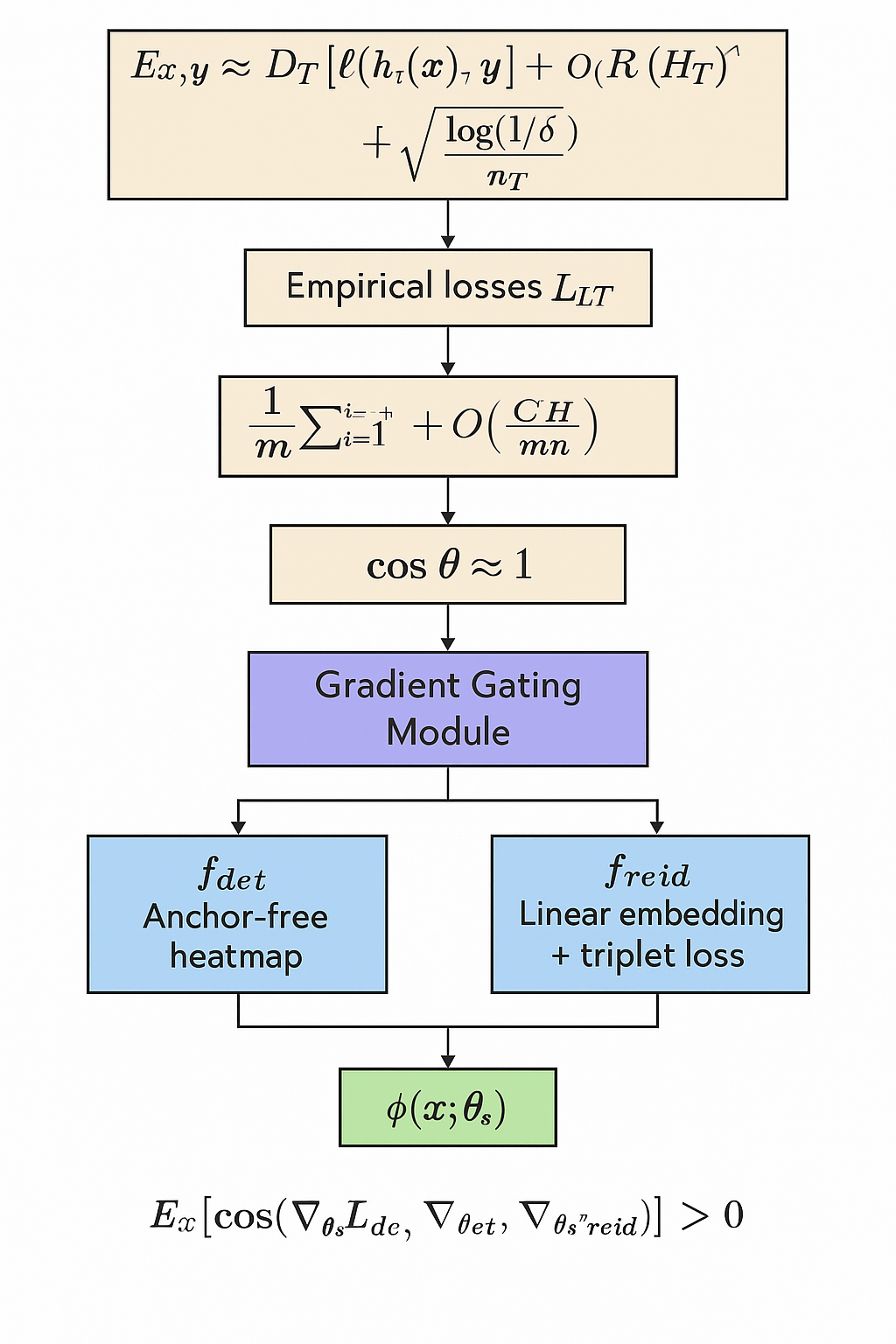
用到的所有算法总结

核心算法1：匈牙利算法用于reID的匹配

匈牙利算法用于解决二分图最大匹配问题，在这里用于目标检测中的匹配任务。

20250707105822

20250707173148

20250707173158

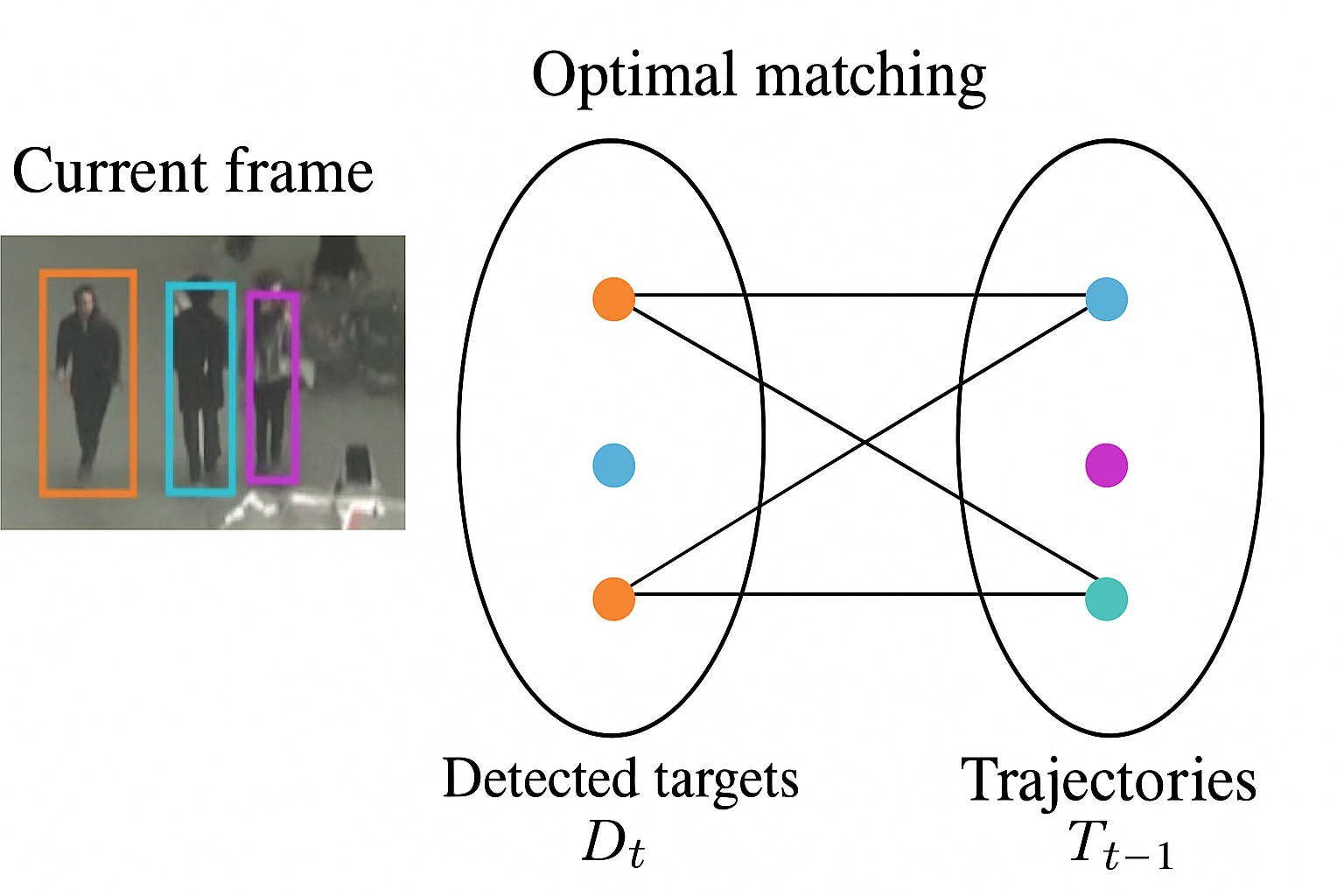
核心算法2：共享的backbone

20250707173208

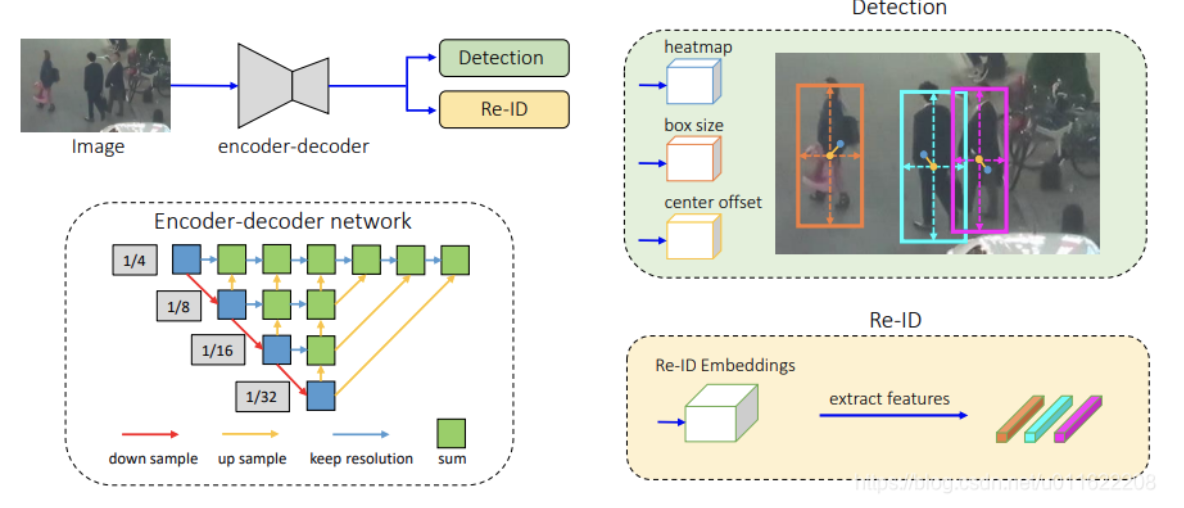
• 输入，经过卷积或其他操作后蕴含高级语义的图像特征图，
• 输出，一个Embedding，蕴含着两大任务：detection和reID所需要的信息。

核心算法3,4,5：统计所有卷积块的作用

• 算法输入：图像特征图，或者说前面提取出来的Embedding

• 算法输出：对于每个检测目标，我们希望网络预测出三个量：

名称	含义	数学符号	监督目标来源	维度
Heatmap	目标中心点概率分布图（高斯图）	Ŷheat ∈ [0, 1]H × W × C	目标中心点位置	每类1通道，共C类
Box Size	对应中心点的物体宽高	Ŷsize ∈ ℝH × W × 2	GT框尺寸 (w, h)	2通道
Offset	浮点中心点误差补偿	Ŷoff ∈ ℝH × W × 2	像素坐标非整点偏移	2通道

这里的 H, W 是输出特征图尺寸（输入图像下采样后的尺寸）

1. Heatmap：预测目标中心点

目标是生成一个类似于热力图的分布，对于每个目标中心点，在其对应位置生成一个高斯峰：

GT 中一个目标中心是 (x_i, y_i)

将它映射到特征图坐标系：(x̂_i, ŷ_i) = (⌊x_i/s⌋, ⌊y_i/s⌋)，s 是下采样倍数

在 (x̂_i, ŷ_i) 周围画一个 半径为 r 的高斯核

构造 heatmap Ŷ ∈ [0, 1]^H × W：中心为 1，周围值小于 1

使用focalloss计算损失

$$\mathcal{L}_{\mathrm{focal}}=\begin{cases}(1-\hat{p}_{xy})^\alpha\log(\hat{p}_{xy})&\mathrm{if}\hat{Y}_{xy}=1\\(1-\hat{Y}_{xy})^\beta(\hat{p}_{xy})^\alpha\log(1-\hat{p}_{xy})&\mathrm{otherwise}\end{cases}$$

其中

• p̂_xy 是网络预测的 heatmap 值

• (x, y) 是中心点（或邻域点）

• α, β 控制正负样本权重

2. Box Size：目标框的 w, h

• 在每个中心点位置 (i, j) 回归其 GT box 的宽高：

  Ŷ_size[i, j] = (w, h)

• 只在目标中心点上进行监督，损失函数使用 ℓ₁ 或 smooth-ℓ₁：

  $$ \mathcal{L}_{\text{size}} = \frac{1}{N} \sum_{(i,j) \in \text{centers}} \left\| \hat{Y}_{\text{size}}[i,j] - (w, h) \right\|_1 $$

Offset：浮点中心点补偿

• 下采样后特征图中只能以整点预测中心点，但实际的中心点坐标是浮点型，所以我们要预测精确位置的偏移量，中心点偏移（offset）是为了补偿下采样导致的小数精度损失。

  $$ \hat{Y}_{\text{off}}[i,j] = \left( \frac{x}{s} - \lfloor \frac{x}{s} \rfloor, \frac{y}{s} - \lfloor \frac{y}{s} \rfloor \right) $$

• 损失函数也是 ℓ₁ 回归：

  $$ \mathcal{L}_{\text{off}} = \frac{1}{N} \sum_{(i,j) \in \text{centers}} \left\| \hat{Y}_{\text{off}}[i,j] - \Delta \right\|_1 $$

网络结构直接输出这三个量

• 网络 backbone（如 DLA-34）提取 feature map；

• 然后通过三个 卷积 head（可以是1-2层的 conv）分别输出：

  Head	输出通道数	用于监督
  Heatmap Head	C	Focal loss
  Size Head	2	box loss
  Offset Head	2	offset loss

import torch
import torch.nn as nn
class Head(nn.Module):
    def __init__(self, in_channels, out_channels):
        super().__init__()
        self.head = nn.Sequential(
            nn.Conv2d(in_channels, 64, 3, padding=1),
            nn.ReLU(),
            nn.Conv2d(64, out_channels, 1)
        )

    def forward(self, x):
        return self.head(x)

# 构造3个head
self.heatmap_head = Head(256, num_classes)
self.size_head = Head(256, 2)
self.offset_head = Head(256, 2)

算法输入是什么？

最终，网络需要对 每个位置 回归：

• 该位置是否为物体中心点（Heatmap）
• 如果是中心点，对应的框大小（Box Size）
• 和实际中心点浮点坐标的偏差（Offset）

Input Image
   ↓
  Backbone (DLA-34)
   ↓
 Feature Map
   ↓
 ┌────────────┬─────────────┬────────────┐
 │ Heatmap    │ Size Head   │ Offset Head│
 │            │             │            │
 ↓            ↓             ↓
C×H×W     2×H×W         2×H×W
 ↓            ↓             ↓
 预测中心概率、预测宽高、预测偏移量

参考文献

[1] Kuhn H W. The Hungarian method for the assignment problem[J]. Naval research logistics quarterly, 1955, 2(1‐2): 83-97.

[2] Cormen T H, Leiserson C E, Rivest R L, et al. Introduction to algorithms[M]. MIT press, 2022.

feat = backbone(x)                         
feat.requires_grad_(True)                 
det_out = det_head(feat)
reid_out = reid_head(feat)
loss_det.backward(retain_graph=True)
grad_det = feat.grad.detach().clone().flatten()
model.zero_grad()

loss_reid.backward(retain_graph=True)
grad_reid = feat.grad.detach().clone().flatten()
model.zero_grad()

# 应用梯度门控模块
gated_feat, gate_val = gcg(grad_det, grad_reid, feat)
det_out = det_head(gated_feat)
reid_out = reid_head(gated_feat)
loss = compute_det_loss(det_out, target_det) + compute_reid_loss(reid_out, target_reid)
loss.backward()
optimizer.step()