源头活水：multilabel-learning（持续更新）

本文持续更新作者在多标签学习领域总结的经典方法（baseline）

MLKNN

ML-KNN 是张敏灵，周志华的大作，是一种基于传统 KNN 的多标签分类扩展算法。 它结合了 KNN 和 贝叶斯推断（Bayesian inference），用于多标签问题，即一个样本可以同时属于多个类别。

基本步骤：

• 先找出每个测试样本的 K 个最近邻。
• 对每个标签，通过 最大后验概率（MAP）推断，判断该标签是否应该赋予这个样本。

为了推导清晰，先设符号：

• ℒ = {l₁, l₂, ..., l_q}：总共有 q 个标签。
• x：测试样本。
• 𝒩(x)：x 的 K 个最近邻。
• c_j ∈ {0, 1}：样本是否属于第 j 个标签。1表示有，0表示没有。
• n_j：在邻居中，有多少个邻居拥有标签 l_j。

对于每个标签 l_j，我们希望计算：

P(c_j = 1 ∣ n_j)  和  P(c_j = 0 ∣ n_j)

即：

• 给定 n_j 个邻居拥有标签 l_j，样本自己拥有/不拥有标签 l_j 的概率。

最后，比较两者大小：

• 如果 P(c_j = 1 ∣ n_j) > P(c_j = 0 ∣ n_j)，就预测有标签。
• 否则预测没有标签。

根据贝叶斯公式：

$$ P(c_j \mid n_j) = \frac{P(n_j \mid c_j) \, P(c_j)}{P(n_j)} $$

注意：

• P(n_j) 在 c_j = 1 和 c_j = 0 的情况下是相同的，因此只比较分子就可以！

• 所以，只需要计算：

  • P(c_j = 1)，先验概率
  • P(n_j ∣ c_j = 1)，似然概率
  • 同理 c_j = 0 时也计算一遍。

从训练集中直接统计得到：

$$ P(c_j=1) = \frac{\text{样本中有标签 } l_j \text{ 的样本数} + s}{\text{总样本数} + 2s} $$

$$ P(c_j=0) = \frac{\text{样本中无标签 } l_j \text{ 的样本数} + s}{\text{总样本数} + 2s} $$

其中 s 是平滑参数（通常 s = 1，防止除零问题）。

同样通过统计得到：

• P(n_j ∣ c_j = 1)：在拥有标签 l_j 的样本中，K个邻居中有 n_j 个拥有标签的概率。
• P(n_j ∣ c_j = 0)：在没有标签 l_j 的样本中，K个邻居中有 n_j 个拥有标签的概率。

具体估计公式：

$$ P(n_j \mid c_j=1) = \frac{\text{在有标签的样本中，邻居数为 } n_j \text{ 的样本数} + s}{\text{有标签的样本总数} + (K+1)s} $$

$$ P(n_j \mid c_j=0) = \frac{\text{在无标签的样本中，邻居数为 } n_j \text{ 的样本数} + s}{\text{无标签的样本总数} + (K+1)s} $$

注意：K + 1 是因为 n_j 可能取值 0, 1, ..., K，一共有 K + 1 个取值。

对每个测试样本 x，每个标签 l_j：

1. 找出 K 个最近邻，统计 n_j。

2. 计算：

   • P(c_j = 1)，P(c_j = 0)
   • P(n_j ∣ c_j = 1)，P(n_j ∣ c_j = 0)

3. 计算后验：

   • P(c_j = 1 ∣ n_j) ∝ P(n_j ∣ c_j = 1) × P(c_j = 1)
   • P(c_j = 0 ∣ n_j) ∝ P(n_j ∣ c_j = 0) × P(c_j = 0)

4. 比较大小，选择最大概率的标签预测。

其实最终判断只用比较：

P(n_j ∣ c_j = 1) × P(c_j = 1)  vs  P(n_j ∣ c_j = 0) × P(c_j = 0)

事实上，MLKNN是利用局部邻居信息，对先验概率（标签占比）进行后验修正。这一方法事实上是单纯的单标签方法，因为这一点，MLKNN也一直收到批评。但是MLKNN是一种懒学习方法，对计算资源要求较低，而且效果相当的不错。

RAKEL

RAKEL是一种集成学习算法，其实是LP方法的进一步发展。LP方法就是把多标签转化为多分类问题，具体的是：把每一种标签组合看成一类，共2^{标签个数 − 1}类。RAKEL为了缓解指数爆炸，通过构建多个子模型并综合结果来提升性能。其关键是通过随机选择标签子集（k-labELset）来捕捉标签间的局部相关性，避免全局计算的复杂性。

算法步骤 1. 生成随机标签子集： • 随机选择大小为k的标签子集（如k=3），生成m个子集，确保每个原始标签被覆盖多次。

• 例如：共有5个标签（A,B,C,D,E），生成子集{A,B,C}、{B,D,E}、{A,C,E}等。

2. 训练子模型： • 对每个k-labELset，使用标签幂集方法将其转换为多类分类问题。

   • 例如：子集{A,B,C}对应8种可能的组合（2^3），训练一个基分类器（如SVM）识别这些组合。实际上解决一个多分类问题

3. 集成预测： • 对测试样本，每个基分类器预测其子集内的标签组合。

   • 通过投票机制汇总结果：统计每个标签的预测频次，超过阈值则判定为关联。

参数选择 • k值：通常取3-5，过小可能忽略依赖，过大增加计算量。

• 子集数量m：需足够覆盖所有标签，经验公式为m ≈ 2L（L为总标签数）。

RAKEL vs. 其他方法对比

方法	处理标签相关性	计算复杂度	适用场景
二元关联 (BR)	忽略	低	标签独立性强
分类器链 (CC)	顺序依赖	中	标签有明确顺序依赖
标签幂集 (LP)	全局组合	高	标签数较少（<20）
RAKEL	局部组合	中-高	中等规模标签（20-100）

分类器链（CC）-> ECC(集成分类器链)

分类器链（Classifier Chains, CC）

算法流程 1. 定义标签顺序：
• 按自然顺序（如标签出现频率）或随机生成顺序（如 y₂ → y₅ → y₁ → ...）。

2. 训练阶段：
   • 对每个标签 y_i：

   ◦ 输入：原始特征 X + 前面标签的真实值 y₁, y₂, ..., y_i − 1（训练时使用真实标签）。

   ◦ 输出：训练一个二分类器（如逻辑回归、SVM）预测 y_i。

3. 预测阶段：
   • 迭代预测：

   1. 预测 y₁：输入仅原始特征 X。
      
   2. 预测 y₂：输入 X + ŷ₁（ŷ₁ 是 y₁ 的预测值）。
      
   3. 依此类推，直到预测完所有标签。
      • 注意：预测时使用前序标签的预测值（而非真实值），因此误差会沿链传播。

示例说明 任务：音乐分类，标签为 {摇滚, 激烈, 人声}。
• 标签顺序：摇滚 → 激烈 → 人声。

• 预测过程：

1. 预测“摇滚”：输入歌曲特征 → 输出 1（是摇滚）。
   
2. 预测“激烈”：输入歌曲特征 + 摇滚=1 → 输出 1（激烈）。
   
3. 预测“人声”：输入歌曲特征 + 摇滚=1 + 激烈=1 → 输出 0（无人声）。
   • 结果：标签为 {摇滚, 激烈}。

优点 1. 捕捉标签依赖：显式利用前序标签信息，提升相关性强的标签预测精度。
2. 灵活性：兼容任意二分类算法作为基分类器。
3. 计算可控：复杂度为 O(L)，适用于中等规模标签（L < 100）。

缺点 1. 误差传播：前序标签预测错误会导致后续标签误差累积。
• 例如：若“摇滚”误判为 0，后续“激烈”可能被错误预测为 0。

2. 顺序敏感性：标签顺序影响模型性能，但最优顺序难以确定。
   
3. 并行性差：链式结构需顺序预测，难以加速。
4. 若标签间独立性较强（如商品属性“颜色”“尺寸”），引入标签作为特征可能引入噪声!

一种成功的改进方法是引入集成学习，创建ECC，通过多条分类器连链投票减少单条分类器链的误差。

BPMLL

BPMLL（Backpropagation for Multi-Label Learning）详解

BPMLL 是一种基于神经网络的多标签分类算法，通过优化标签排序损失函数直接建模多标签间的复杂依赖关系

算法原理

输出层：每个标签对应一个神经元，输出值表示该标签的相关性得分（未归一化）。

2. 损失函数 BPMLL 使用成对排序损失函数（Pairwise Ranking Loss），目标是让相关标签的得分高于无关标签的得分。具体公式如下：

$$ \text{Loss} = \sum_{i=1}^N \sum_{(y^+, y^-) \in Y_i^+ \times Y_i^-} \exp\big(-(f(x_i, y^+) - f(x_i, y^-))\big) $$ • N：样本数。

• Y_i⁺：样本 i 的相关标签集合。

• Y_i⁻：样本 i 的无关标签集合。

• f(x_i, y)：网络对样本 x_i 在标签 y 上的得分。

优化目标：最小化相关标签与无关标签的得分差异，使得对每个样本，所有相关标签的得分均高于无关标签。

3. 训练流程 1. 前向传播：计算所有标签的得分。
2. 损失计算：根据成对排序损失，计算所有相关-无关标签对的损失。
3. 反向传播：通过梯度下降更新网络权重。
4. 预测：对测试样本，按标签得分从高到低排序，取前 k 个或超过阈值的标签。

优点 1. 捕捉标签依赖：
通过全局优化直接建模标签间复杂的依赖关系（如排斥、共现），无需手动设计链式或组合策略。
2. 排序信息利用：
输出标签的排序结果，适用于需要优先级判断的场景（如推荐系统）。
3. 灵活性高：
兼容任意神经网络结构（如 CNN、RNN），适合处理图像、文本等复杂数据。

缺点 1. 计算复杂度高：
成对损失需要对所有相关-无关标签对计算损失，当标签数 L 较大时，复杂度为 O(L²)，训练效率低。
例如：若 L = 1000，每样本需处理约 500 × 500 = 250, 000 对，计算量巨大。
2. 阈值敏感：
预测时需设定阈值或选择前 k 个标签，阈值选择影响最终性能。

代码

import torch
import torch.nn as nn
import torch.optim as optim

class BPMLL(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim):
        super(BPMLL, self).__init__()
        self.fc1 = nn.Linear(input_dim, hidden_dim)
        self.fc2 = nn.Linear(hidden_dim, output_dim)
        self.relu = nn.ReLU()

    def forward(self, x):
        x = self.relu(self.fc1(x))
        x = self.fc2(x)
        return x  


def bp_mll_loss(outputs, targets):
    loss = 0.0
    for i in range(outputs.size(0)):
        pos = targets[i] == 1
        neg = targets[i] == 0
        for y_plus in outputs[i][pos].tolist():
            for y_minus in outputs[i][neg].tolist():
                loss += torch.exp(-(y_plus - y_minus))
    return loss / outputs.size(0)


model = BPMLL(input_dim=100, hidden_dim=64, output_dim=10)
optimizer = optim.Adam(model.parameters(), lr=0.001)

for epoch in range(100):
    for X_batch, y_batch in dataloader:
        scores = model(X_batch)
        loss = bp_mll_loss(scores, y_batch)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

20250505192405

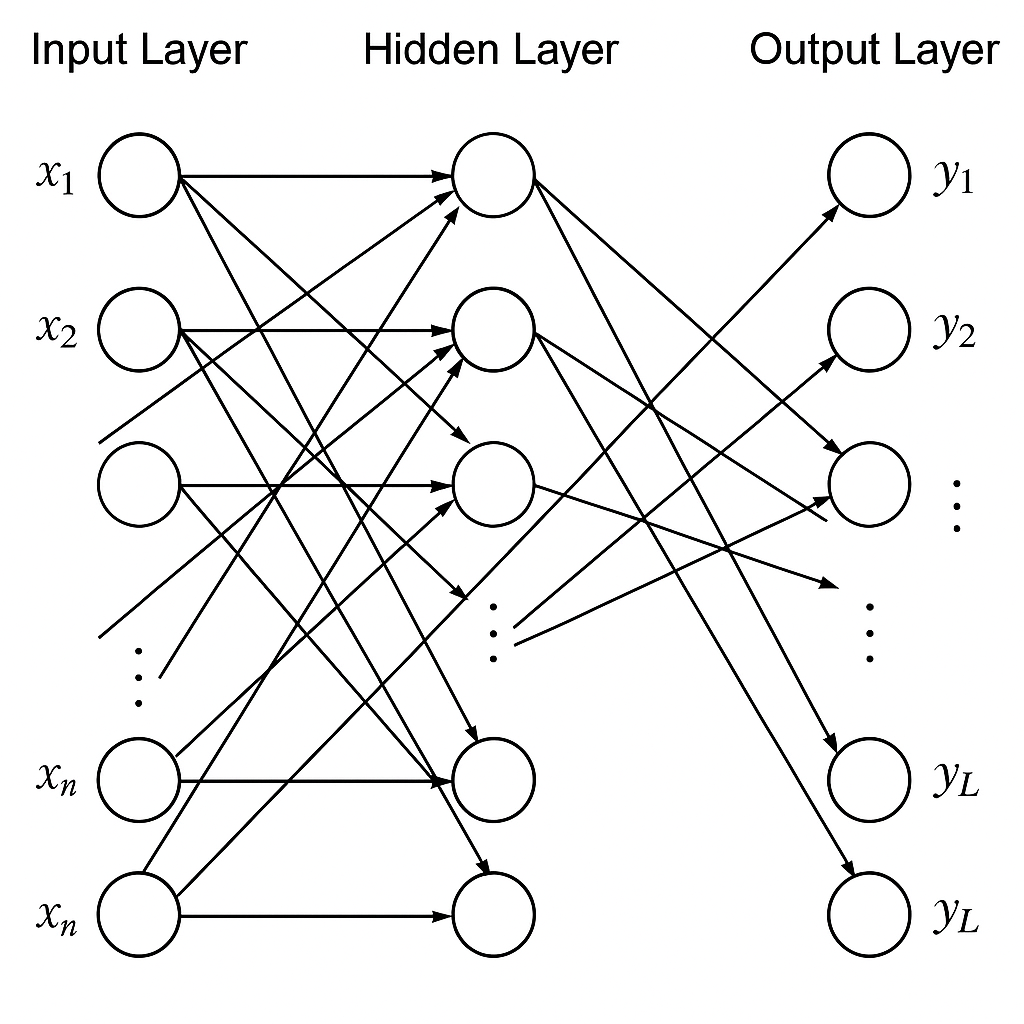
SVM发展得来的方法

1.1Rank-SVM

我们想要将svm方法引入多标签问题，rank-svm是一个成功的例子。 针对多标签学习问题（实例可同时关联多个标签），Rank-SVM通过引入排序机制扩展传统SVM。其核心思想为：对每个标签学习独立的分类器，并通过约束强制正标签得分高于负标签。

设数据集包含Q个标签，优化问题表述为： $$ \begin{aligned} \min_{\boldsymbol{w}_k,\xi_{ikl}} &\quad \frac{1}{2}\sum_{k=1}^Q \|\boldsymbol{w}_k\|^2 + C\sum_{i=1}^m \frac{1}{|Y_i||\bar{Y}_i|}\sum_{(k,l)\in Y_i\times\bar{Y}_i} \xi_{ikl} \\ \text{s.t.} &\quad \langle \boldsymbol{w}_k, \boldsymbol{x}_i \rangle - \langle \boldsymbol{w}_l, \boldsymbol{x}_i \rangle \geq 1 - \xi_{ikl} \\ &\quad \xi_{ikl} \geq 0,\quad \forall i\in\{1,...,m\},\ (k,l)\in Y_i\times\bar{Y}_i \end{aligned} $$

1. 排序约束：对每个样本x_i，其相关标签k ∈ Y_i的得分需高于无关标签l ∈ Ȳ_i至少1个边际单位
2. 正则化项：$\frac{1}{2}\sum\|\boldsymbol{w}_k\|^2$控制模型复杂度，防止过拟合
3. 排序损失：∑ξ_ikl量化违反排序约束的惩罚，系数$\frac{1}{|Y_i||\bar{Y}_i|}$实现样本间归一化

时间复杂度分析

相较于单标签SVM，Rank-SVM复杂度显著增加：每个样本产生|Y_i|×|Ȳ_i|个约束，总约束数达： $$ N_{\text{constr}} = \sum_{i=1}^m |Y_i|(Q-|Y_i|) \approx O(mQ^2) $$ 当标签数Q较大时，约束规模呈平方增长问题求解的时间复杂度为： O(N_constr³) = O(m³Q⁶)

1.2 KNN加权单SVM分类器

多标签TSVM加权

介绍两种结构用于建模label信息。

local geometric information

对于标签r定义两种边。i，j是对应于label:r的实例，而l是不对应label:r的实例。

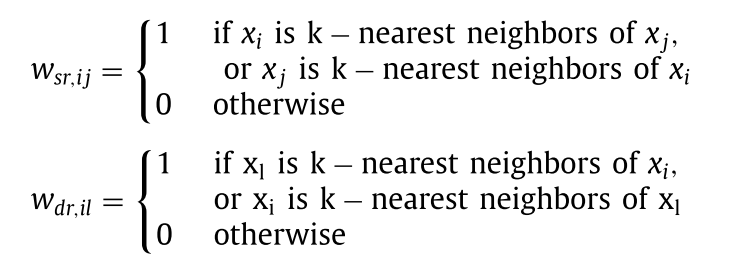
第一种边对应r的类内关系，第二种边对应r内与非r样本的类间关系。

作者还定义了 $$f_{rl}=\begin{cases}1&\mathrm{if~}\exists i,w_{dr,il}\neq0\\0&\mathrm{otherwise}&\end{cases}$$ 用于衡量类r与任意的非r样本l之间的关系，若l在kNN的意义上距离r类足够近则该边为1.

structural information in samples

对于任意一个类r，将其ward聚类为若干个簇C_i,定义 $$\begin{aligned}&u_{C_{i}}=\frac{1}{|C_i|}\sum_{x_j\in C_i}x_j\\&\Sigma_{C_{i}}=\frac{1}{|C_i|}\sum_{x_j\in C_i}\left(x_j-u_{C_i}\right)\left(x_j-u_{C_i}\right)^T\end{aligned}$$ 并以矩阵 Σ_r = Σ_C1 + … + Σ_CΛr 定义结构信息。

作者最终模型是这样的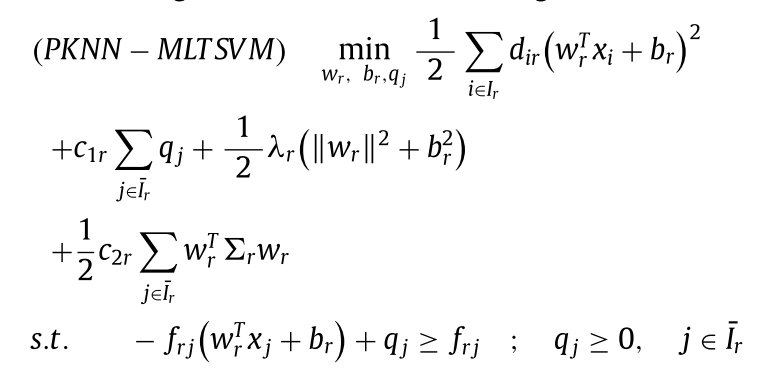

加权在以下 个方面

• d_ir = ∑_j ∈ Irw_sr, ij加权距离贴近，与上篇类似，用有多少个KNN近邻点衡量样本x_i之于label : r的重要性，邻居越多则越该被正确分类。

• 项 $\frac{1}{2}c_{2r}\sum_{j\in\bar{I}_r}w_r^T\Sigma_rw_r$ 的目的是通过结构化正则化约束分类超平面，使其与类别 r 的数据分布特性对齐。具体解释如下（deepseek）：

1. 协方差矩阵 Σ_r 的物理意义

• 结构信息表示：Σ_r = Σ_C1 + … + Σ_CΛr 是类别 r 中所有子簇协方差矩阵的和，反映了该类别数据的整体分布特性。若数据在某一方向上的方差较大（即 Σ_r 对应特征值较大），则表明该方向数据分布较分散。
• 局部结构捕捉：通过 Ward 聚类将类别 r 划分为多个子簇，Σ_r 能够刻画类内数据的局部几何结构（如多模态分布或异质子群）。 ### 2. 优化项的作用
• 结构化正则化：该项本质是数据依赖的正则化项，与传统的 L₂ 正则化（如 ∥w_r∥²）不同，它通过 Σ_r 对不同方向施加自适应的惩罚。
  
• 若某方向数据方差大（Σ_r 特征值大），则在该方向上 w_r 的权重会被更严格约束，避免过拟合噪声或异常点。
• 若某方向方差小（特征值小），则允许 w_r 在该方向有更大权重，从而更贴合数据的紧密分布。
• 理论依据：
  这一设计符合结构风险最小化原则，即通过引入先验知识（数据分布的结构信息）来约束模型复杂度，提升泛化能力。类似思想在流形学习（如 LDA 的类内散度矩阵）和鲁棒优化中均有体现。 ### 3. 多标签分类中的意义 在多标签场景下，不同标签可能对应不同的数据分布模式：
• 独立性假设：每个标签的超平面独立优化，Σ_r 仅关注当前标签的数据结构，避免其他标签的干扰。
• 鲁棒性增强：通过显式建模类内结构，超平面能更好适应复杂分布（如多簇、非高斯分布），从>而提升对噪声和异常值的鲁棒性。

• 由于f_rj用于衡量衡量类r与任意的非r样本l之间的关系,用于增强局部可分性