时间序列

ARIMA模型

AR模型（自回归）

简单来说，就是利用过去最近的时刻p个时刻的标签来对需要预测的时刻进行线性回归

Y_t = c + φ₁Y_t − 1 + φ₂Y_t − 2 + … + φ_pY_t − p + ξ_t

其中ξ_t表示噪声 ，p为模型的可调参数

对于模型的设立，有两点基本假设

• 时序依赖性：假设不同时间点的标签值之间存在强相关性。
• 时序衰减：两个时间点之间的距离越远，他们之间的关联性越弱。例如，昨天的天气可能对今天的天气影响很大，但三个月前的某一天的天气，对今天的天气的影响就相对微弱。

AR( p )模型模型在时间区间[0,t]上进行训练，在时间区间[t+1,t+m]上进行预测

train

$$ \begin{aligned} &Y_{1}=c+\varphi_1Y_0\\ &Y_{2}=c+\varphi_1Y_1+\varphi_2Y_0\\ &Y_{3}=c+\varphi_1Y_2+\varphi_2Y_1+\varphi_3Y_0\\ &Y_{t}=c+\varphi_1Y_{t-1}+\varphi_2Y_{t-2}+\ldots+\varphi_pY_{t-p} \end{aligned} $$

predict

$$\begin{aligned}&\hat{Y}_{t+1}=c+\varphi_1Y_t+\varphi_2Y_{t-1}+\ldots+\varphi_pY_{t-p+1}\\&\hat{Y}_{t+2}=c+\varphi_1\hat{Y}_{t+1}+\varphi_2Y_t+\ldots+\varphi_pY_{t-p+2}\\&\hat{Y}_{t+3}=c+\varphi_1\hat{Y}_{t+2}+\varphi_2\hat{Y}_{t+1}+\ldots+\varphi_pY_{t-p+3}\\&\hat{Y}_{t+m}=c+\varphi_{1}\hat{Y}_{t+m-1}+\varphi_{2}\hat{Y}_{t+m-2}+\ldots+\varphi_{p}\hat{Y}_{t+m-p}\end{aligned}$$

MA模型（移动平均）

MA模型的基本思想和基本假设与AR模型大不相同。MA模型的基本思想是：大部分时候时间序列应当是相对稳定的。在稳定的基础上，每个时间点上的标签值受过去一段时间内、不可预料的各种偶然事件影响而波动。即在一段时间内，时间序列应该是围绕着某个均值上下波动的序列，时间点上的标签值会围绕着某个均值移动，因此模型才被称为“移动平均模型 Moving Average Model”

给定噪声序列ϵ_tMA模型定义为： Y_t = μ + ϵ_t + θ₁ϵ_t − 1 + θ₂ϵ_t − 2 + ⋯ + θ_qϵ_t − q

模型基于三点基本假设 - 均值稳定：时间序列应该是围绕着某个均值上下波动的序列 - 方差稳定 - 无自相关性：不同时间点的观察值之间没有自相关性

ARIMA模型

• AR模型，即自回归模型，其优势是对于具有较长历史趋势的数据，AR模型可以捕获这些趋势，并据此进行预测。但是AR模型不能很好地处理某些类型的时间序列数据，例如那些有临时、突发的变化或者噪声较大的数据。AR模型相信“历史决定未来”，因此很大程度上忽略了现实情况的复杂性、也忽略了真正影响标签的因子带来的不可预料的影响。

• 相反地，MA模型，即移动平均模型，可以更好地处理那些有临时、突发的变化或者噪声较大的时间序列数据。但是对于具有较长历史趋势的数据，MA模型可能无法像AR模型那样捕捉到这些趋势。MA模型相信“时间序列是相对稳定的，时间序列的波动是由偶然因素影响决定的”，但现实中的时间序列很难一直维持“稳定”这一假设。

基于以上两个模型的优缺点，我们引入了ARIMA模型，这是一种结合了AR模型和MA模型优点的模型，可以处理更复杂的时间序列问题。ARIMA模型主要由三部分构成，分别为自回归模型（AR）、差分过程（I）和移动平均模型（MA）

• ARIMA模型的基本思想是利用数据本身的历史信息来预测未来。一个时间点上的标签值既受过去一段时间内的标签值影响，也受过去一段时间内的偶然事件的影响，这就是说，ARIMA模型假设：标签值是围绕着时间的大趋势而波动的，其中趋势是受历史标签影响构成的，波动是受一段时间内的偶然事件影响构成的，且大趋势本身不一定是稳定的

暂时不考虑差分（即假设d=0），那么ARIMA模型可以被看作是AR模型和MA模型的直接结合，也也就是利用AR模型对MA模型的μ建模，形式上看，ARIMA模型的公式可以表示为： Y_t = c + φ₁Y_t − 1 + φ₂Y_t − 2 + … + φ_pY_t − p + θ₁ϵ_t − 1 + θ₂ϵ_t − 2 + … + θ_qϵ_t − q + ϵ_t

如果考虑差分，那么完整的ARIMA表示为： Δ^dY_t = ϕ₁Y_t − 1 + ϕ₂Y_t − 2 + ⋯ + ϕ_pY_t − p + ϵ_t + θ₁ϵ_t − 1 + θ₂ϵ_t − 2 + ⋯ + θ_qϵ_t − q

• Δ^dY_t表示进行了d次差分后的平稳序列；

• ϕ₁, ϕ₂, …, ϕ_p是自回归项的系数；

• θ₁, θ₂, …, θ_q是移动平均项的系数；

• ϵ_t是随机误差项。

参数选取

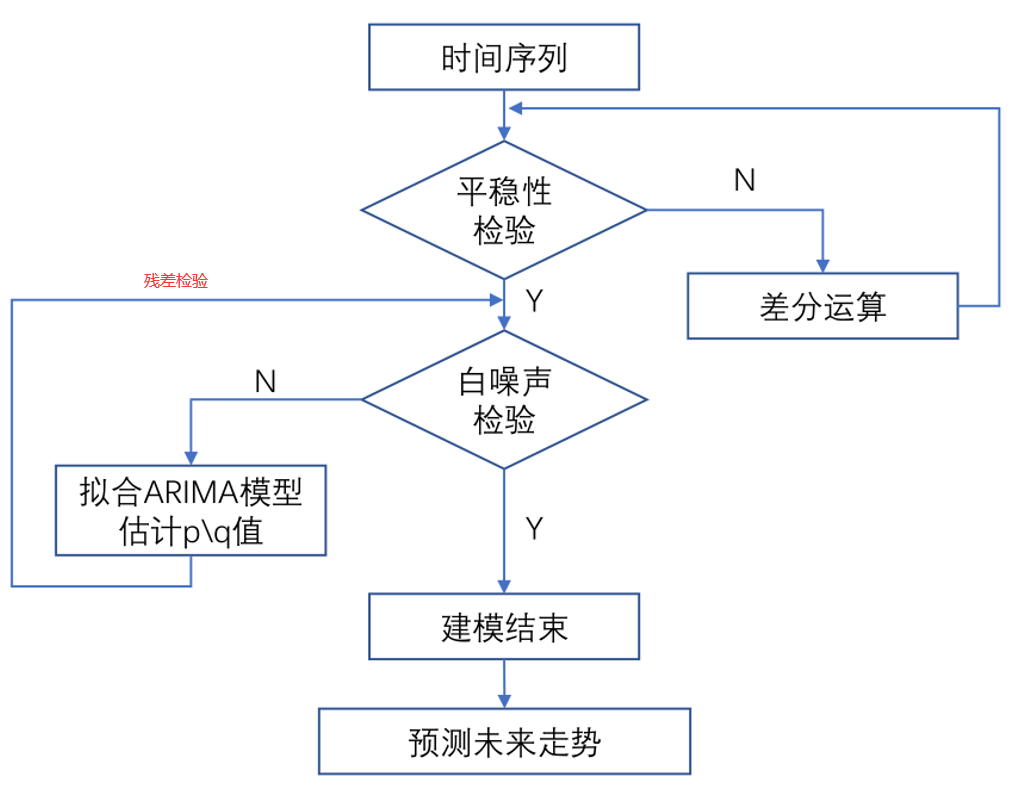
模型有三个可调参数p,q,d - p 代表 “自回归部分 (Autoregressive)”： 这部分描述了模型中使用的观测值的滞后值（即前面 p 个期的值）。自回归模型的出发点是认为观测值是它前面的 p 个值的线性组合。 - q 代表 “移动平均部分 (Moving Average)”：这部分描述了模型中使用的错误项的滞后值（即前面 q 个期的值）。移动平均模型是将当前值和过去的白噪声之间建立关系。 - d就是差分的阶数。差分的目标是将非平稳序列转变为平稳序列。

先确定d

确定d值（差分次数）：通过平稳性检验（ADF检验）或观察时间序列的自相关图（ACF图）和偏自相关图（PACF图）来判断。若序列非平稳，则进行差分处理，直至序列平稳。 通常采用ADF检验

import numpy as np
import pandas as pd
from statsmodels.tsa.stattools import adfuller
import matplotlib.pyplot as plt

def plot_sales(df, title='Sales Data'):
    """辅助函数：绘制时间序列图"""
    plt.figure(figsize=(10, 6))
    plt.plot(df.index, df['Sales'], marker='o', label='Sales')
    plt.title(title)
    plt.xlabel('Year')
    plt.ylabel('Sales')
    plt.grid(True)
    plt.legend()
    plt.show()

def adf_test(series, signif=0.05, name=''):
    """辅助函数：执行ADF单位根检验并打印结果"""
    result = adfuller(series.dropna(), autolag='AIC')  # 使用AIC准则选择滞后长度
    output = pd.Series(result[0:4], index=['Test Statistic', 'p-value', 'Lags Used', 'Number of Observations'])
    for key, value in result[4].items():
        output[f'Critical Value ({key})'] = value
    print(f'\nADF Test Result ({name}):')
    print(output.to_string())
    
    p_value = result[1]
    if p_value <= signif:
        print(f" => Null Hypothesis REJECTED - Data {name} has no unit root and is stationary.")
    else:
        print(f" => Null Hypothesis ACCEPTED - Data {name} has a unit root and is non-stationary.")

def find_optimal_differences(series, max_d=2, plot=True):
    """确定最佳差分阶数d"""
    original_series = series.copy()
    for d in range(max_d + 1):
        if d > 0:
            series = series.diff().dropna()
            if plot:
                plot_sales(pd.DataFrame({'Sales': series}), f'Differenced Time Series (Order {d})')
        
        adf_test(series, name=f'after {d} difference(s)')
        
        # 检查是否已经达到了平稳性
        if adfuller(series)[1] <= 0.05:
            print(f"\nThe optimal differencing order is {d}.")
            break
    else:
        print(f"\nCould not achieve stationarity within {max_d} differences.")
    
    return d, series

# 创建年度销量数据并转换为DataFrame
data = {
    'Year': list(range(1985, 2022)),
    'Sales': [
        100, 101.6, 103.3, 111.5, 116.5, 120.1, 120.3, 100.6, 83.6, 84.7,
        88.7, 98.9, 111.9, 122.9, 131.9, 134.2, 131.6, 132.2, 139.8, 142,
        140.5, 153.1, 159.2, 162.3, 159.1, 155.1, 161.2, 171.5, 168.4, 180.4,
        201.6, 218.7, 247, 253.7, 261.4, 273.2, 279.4
    ]
}
df = pd.DataFrame(data).set_index('Year')

# 绘制原始时间序列图
plot_sales(df, 'Original Time Series')

# 查找最优差分阶数
optimal_d, final_series = find_optimal_differences(df['Sales'], max_d=2)

# 如果需要可以在这里继续使用final_series进行进一步分析...
 ```    

### 确定q,p

一种方法是使用拖尾，截尾法，但是主观性强，通常使用AIC和BIC网格搜索.
```py
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from statsmodels.tsa.arima.model import ARIMA
from tqdm import tqdm
import warnings


# 忽略警告信息
warnings.filterwarnings("ignore")


# 创建年度销量数据
data = {
    'Year': [
        1985, 1986, 1987, 1988, 1989, 1990, 1991, 1992, 1993, 1994, 
        1995, 1996, 1997, 1998, 1999, 2000, 2001, 2002, 2003, 2004,
        2005, 2006, 2007, 2008, 2009, 2010, 2011, 2012, 2013, 2014, 
        2015, 2016, 2017, 2018, 2019, 2020, 2021
    ],
    'Sales': [
        100, 101.6, 103.3, 111.5, 116.5, 120.1, 120.3, 100.6, 83.6, 84.7, 
        88.7, 98.9, 111.9, 122.9, 131.9, 134.2, 131.6, 132.2, 139.8, 142,
        140.5, 153.1, 159.2, 162.3, 159.1, 155.1, 161.2, 171.5, 168.4, 180.4,
        201.6, 218.7, 247, 253.7, 261.4, 273.2, 279.4
    ]
}


# 将数据转化为Pandas DataFrame
df = pd.DataFrame(data)
df.set_index('Year', inplace=True)


# 定义差分阶数 d
d = 1  # 根据ADF准则求出的最佳差分阶数  


# 对数据进行 d 阶差分操作
df_diff = df['Sales']
for _ in range(d):
    df_diff = df_diff.diff().dropna()


# 准备存储AIC和BIC值
aic_values = []
bic_values = []
p_values = range(0,7)  # 选择不同的AR阶数
q_values = range(0,7)  # 选择不同的MA阶数


# 存储AIC和BIC值的矩阵
aic_matrix = np.zeros((len(p_values), len(q_values)))
bic_matrix = np.zeros((len(p_values), len(q_values)))


# 遍历不同的AR和MA阶数，拟合ARIMA模型并记录AIC和BIC值
with tqdm(total=len(p_values) * len(q_values)) as pbar:
    for i, p in enumerate(p_values):
        for j, q in enumerate(q_values):
            try:
                model = ARIMA(df_diff, order=(p, 1, q))  # 这里d=1代表差分
                results = model.fit()
                aic_matrix[i, j] = results.aic
                bic_matrix[i, j] = results.bic
                aic_values.append((p, q, results.aic))
                bic_values.append((p, q, results.bic))
            except:
                pass
            pbar.update(1)


# 找到AIC最小值对应的(p, q)
aic_min_index = np.argmin(np.array(aic_values)[:, 2])
p_aic_min, q_aic_min, aic_min_value = np.array(aic_values)[aic_min_index]

print(f"Optimal ARIMA order (p, q) using AIC: ({p_aic_min}, 1, {q_aic_min})")


# 找到BIC最小值对应的(p, q)
bic_min_index = np.argmin(np.array(bic_values)[:, 2])
p_bic_min, q_bic_min, bic_min_value = np.array(bic_values)[bic_min_index]

print(f"Optimal ARIMA order (p, q) using BIC: ({p_bic_min}, 1, {q_bic_min})")

# 创建一个新的图形，设置为3D
fig = plt.figure(figsize=(15, 7))


# 绘制AIC的3D图
ax1 = fig.add_subplot(121, projection='3d')
p_grid, q_grid = np.meshgrid(p_values, q_values)
surf_aic = ax1.plot_surface(p_grid, q_grid, aic_matrix, cmap='viridis')
ax1.set_title('AIC Criterion for ARIMA(p, d=1, q)')
ax1.set_xlabel('AR order (p)')
ax1.set_ylabel('MA order (q)')
ax1.set_zlabel('AIC Value')
fig.colorbar(surf_aic, ax=ax1, label='AIC Value')


# 绘制BIC的3D图
ax2 = fig.add_subplot(122, projection='3d')
surf_bic = ax2.plot_surface(p_grid, q_grid, bic_matrix, cmap='plasma')
ax2.set_title('BIC Criterion for ARIMA(p, d=1, q)')
ax2.set_xlabel('AR order (p)')
ax2.set_ylabel('MA order (q)')
ax2.set_zlabel('BIC Value')
fig.colorbar(surf_bic, ax=ax2, label='BIC Value')


plt.tight_layout()
plt.show()

最后进行预测即可