线性规划

规划基本概念

• 定义：在给定的约束条件(constraint)下，找出一个决策变量(decision variable)的值，使得被称为目标函数(objective function)的表达愿望尺度的函数值达到最小或最大。
• 在解决实际问题时，把问题归结成一个最优化模型是很重要的一步，也是很困难的一步，模型建立得是否恰当，直接影响到求解。建立模型的关键之一是选择适当的决策变量。 $$\begin{array}{ll}\min&f(\mathbf{x})\\\mathrm{s.t.}&\mathbf{x}\in S\subset\mathbb{R}^n.\end{array}$$ 在此，目标函数f是定义在包含S的适当集合上的实值函数。 进一步，S是该问题变量x的可取值之集合，称为问题的可行域(feasible region)。 满足约束条件x ∈ S的x称为问题的可行解(feasible solution)。 在所有可行解中包含局部最优解和全局最优解，我们的目的就是找到全局最优解。
• 带约束最优化问题通常可写为： $$\begin{array}{ll}\min&f(\mathbf{x})\\\mathrm{s.t.}&c_i(\mathbf{x})=0,\quad i\in E,\\&c_i(\mathbf{x})\geqslant0,\quad i\in I.\end{array}$$

在matlab中常用的对应工具包 - 1.非线性规划 fmincon - 2.无约束极值 fminunc, fminsearch - 3.二次规划问题(目标函数是二次函数，约束条件全部是线性的) quadprog , - 4.其它 fseminf (半无穷约束条件), - 5 fminimax min_xmax_iF_i(x)

线性规划

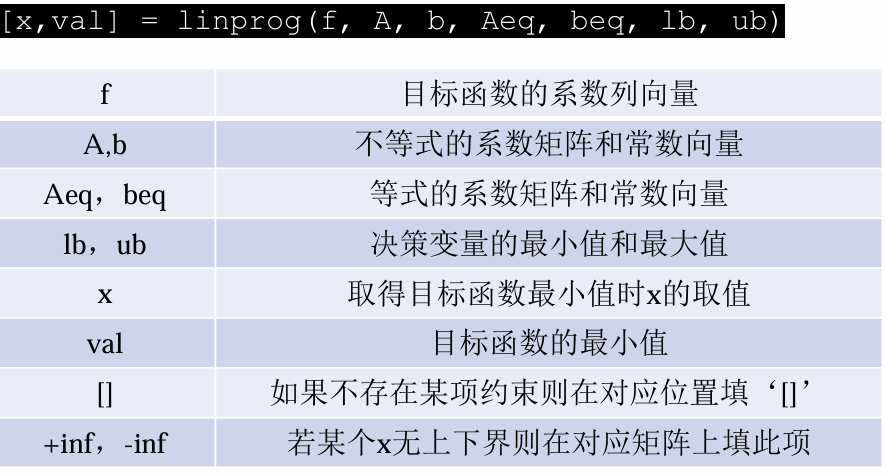
把所有的方程约束中系数做成系数矩阵A_eq，等号右边的常数作为列向量b_eq；不等式约束中的系数矩阵A和不等号右边的常数b，为了方便起见通常将不等式统一为小于等于；变量x在向量l_b到u_b之间取值；目标函数的系数向量为c，那么线性规划的标准形式(也是matlab标准形式)就如下所示： $$\min_x\{f^Tx\}\\s.t.\begin{cases}A\cdot x\leq b\\A_{eq}\cdot x=b_{eq}\\l_b\leq x\leq u_b\end{cases}$$

matlab求解

• 含有绝对值的将问题转化为线性规划 $$\begin{array}{l}\min\{z=|x_1|+|x_2|+\cdots+|x_n|\}\\s.t.Ax\leq b\end{array}$$

其中x = (x₁, x₂, ⋯, x_n)^T。

取： $$u_i=\dfrac{x_i+|x_i|}{2},v_i=\dfrac{|x_i|-x_i}{2}$$
则： u_i ≥ 0, v_i ≥ 0, x_i = u_i − v_i, |x_i| = u_i + v_i
原始优化问题化为： $$\operatorname*{min}\{z=\sum_{i=1}^n(u_i+v_i)\}\\s.t.\begin{cases}A(u-v)\leq b\\u,v\geq0\end{cases}$$ 其中u = (u₁, u₂, ⋯, u_n)^T, v = (v₁, v₂, ⋯, v_n)^T. 进一步可以写成 $$\min\{z=\sum_{i=1}^n(u_i+v_i)\}\\s.t.\begin{cases}(A,-A)\begin{pmatrix}u\\v\end{pmatrix}\le b\\[2ex]u,v\ge0\end{cases}$$

• 例2.市场上有n 种资产s_i(i = 1, 2, · · ·, n)可以选择，现用数额为M的相当大的资金作一个时期的投资。这n 种资产在这一时期内购买s_i的平均收益率为r_i,风险损失率为q_i,投资越分散，总的风险越少，总体风险可用投资的s_i中最大的一个风险来度量.购买s_i时要付交易费，费率为p_i。另外，假定同期银行存款利率是r₀,既无交易费又无风险(r₀ = 5%) 已知n = 4时相关数据如表1.1所列.请你为该公司设计一种投资方案，使净收益尽可能大，总体风险尽可能小.

$$\text{目标函数}\begin{cases}\max\sum_{i=0}^n(r_i-p_i)x_i\\\\\min\left\{\max_{1\leqslant i\leqslant n}\left\{q_ix_i\right\}\right\}\end{cases},\text{ 约束条件为}\begin{cases}\sum_{i=0}^n(1+p_i)x_i=M,\\\\x_i\geqslant0,i=0,1,\cdots,n_\circ&\end{cases}$$

但是两个目标函数求解不了，为此我们考虑把一个目标函数转化为约束条件即可

$$\begin{cases}\sum_{i=0}^n(1+p_i)x_i=M,\\x_i\geqslant0,i=0,1,\cdots,n\\\frac{q_ix_i}M\leqslant a\end{cases}$$

运输问题 (产销平衡) & 指派问题

• 运输问题 某商品有m个产地、n个销地，各产地的产量分别为a₁, ⋯, a_m,各销地的需求量分别为b₁, · · ·, b_n。若该商品由i产地运到 j 销地的单位运价为c_ij ,问应该如何调运才能使总运费最省？
  解：引入变量x_i,其取值为由i产地运往 j 销地的该商品数量，数学模型为 $$\begin{aligned}&\text{min}\quad\sum_{i=1}^m\sum_{j=1}^nc_{ij}x_{ij}\\&\text{s.t.}\quad\begin{cases}\sum_{j=1}^nx_{ij}=a_i,&i=1,\cdots,m\\\\\sum_{i=1}^mx_{ij}=b_j,&j=1,2,\cdots,n\\\\x_{ij}\geq0\end{cases}\end{aligned}$$

• 指派问题 例 7 拟分配n 人去干n 项工作，每人干且仅干一项工作，若分配第i 人去干第 j 项工作，需花费c_ij单位时间，问应如何分配工作才能使工人花费的总时间最少？ 容易看出，要给出一个指派问题的实例，只需给出矩阵C = (c_ij), C被称为指派 问题的系数矩阵。 引入变量x_ij,若分配i干j 工作，则取x_ij = 1,否则取x_ij = 0。上述指派问题的 数学模型为 $$\begin{aligned} &\mathrm{min}\quad\sum_{i=1}^{n}\sum_{j=1}^{n}c_{ij}x_{ij} \\ \text{s.t.}& \sum_{j=1}^{n}x_{ij}=1 \\ &\sum_{i=1}^{n}x_{ij}=1 \\ &x_{ij}=0 \text{或} 1 \end{aligned}$$

对 于指派问题等 0−1整数规划问题，可以直接利用 Matlab 的函数 bintprog 进行求解。

• 匈牙利算法：