降维

协方差矩阵

方差：单个向量/变量序列

$$\mathrm{Var(a)=\frac{1}{m}.\sum_{i=1}^{m}~(a_{i}-\mu)^{2}}$$ 对于质心系的坐标，可以直接写为 $$\mathrm{Var(a)=\frac{1}{m}.\sum_{i=1}^{m}~a_{i}^{2}}$$

协方差(covariance)：两个向量

协方差用来描述两个向量之间的相关性，在PCA中我们希望降维后的变量可以保存更多的原始信息，所以尽可能的减少变量之间的相关性，因为相关性越大，则就代表着两个变量不是完全独立的，也即必然有重复的信息。 $$\mathrm{Cov(a,b)=\frac1{m-1}.\sum_{i=1}^m~(a_i-\mu_a)(b_i-\mu_b)}$$ 对于已经归中的数据，可以写为(较大维度情况下m与m-1差别不大) $$\mathrm{Cov(a,b)=\frac{1}{m}.\sum_{i=1}^{m}a_{i}b_{i}}$$

协方差可以衡量两个向量(变量)同时变化的程度，若协方差cov(a,b)>0，则表示a若增大，b也增大；小于0时，a增大，b减小。 后话：当协方差为0的时候，也即表示两个变量之间不相关。在PCA降维时，就是选择几个基，使得原始数据变换到该组基上时，各变量之间的协方差为零，而变量的方差却很大。 而为了让协方差为0，选择第二个基的时候，与第一个基正交，第三个与第二个正交，这样两两正交的基，最后的相关性就是0。

协方差矩阵 ：多个向量

上述只是单个向量的方差和两个向量之间的协方差，若有多个向量，则可以用矩阵来表示两两的相关性。如有向量a,b,c，用矩阵X表示这三个向量，则其两两之间的协方差可以用矩阵来表示。

$$\mathrm{X=\begin{pmatrix}a\\b\\c\end{pmatrix}=\begin{pmatrix}a_1&a_2&a_3&...\\b_1&b_2&b_3&...\\c_1&c_2&c_3&...\end{pmatrix}}\\\\\\\mathrm{cov(X)=\begin{pmatrix}cov(a,a)&cov(a,b)&cov(a,c)\\cov(b,a)&cov(b,b)&cov(b,c)\\cov(c,a)&cov(c,b)&cov(c,c)\end{pmatrix}}$$

去了均值后的协方差就是向量的内积求平均

1724862185379.png

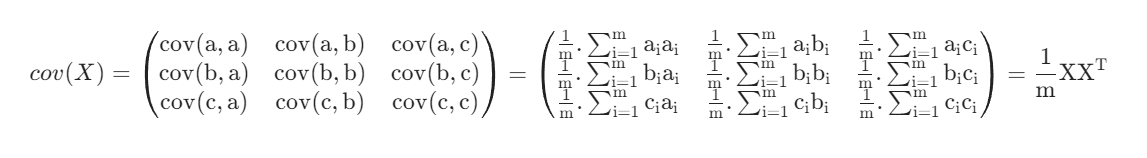
背景引入：维度灾难

边长为R的球与其外接立方体在n维空间中的体积比为 $$\lim_{n\to0}\frac{CR^n}{2^nR^n}=0$$ 这意味着高维空间中数据往往分布在边缘，因此，对于高维数据的降维处理是很有必要的

主成分分析

必要的，先对协方差矩阵做一些变形

$$\begin{aligned} \text{S}& =\frac1N\sum_{i=1}^N(x_i-\overline{x})(x_i-\overline{x})^T \\ &=\frac1N(x_1-\overline{x},x_2-\overline{x},\cdots,x_N-\overline{x})(x_1-\overline{x},x_2-\overline{x},\cdots,x_N-\overline{x})^T \\ &=\frac1N(X^T-\frac1NX^T\mathbb{I}_{N1}\mathbb{I}_{N1}^T)(X^T-\frac1NX^T\mathbb{I}_{N1}\mathbb{I}_{N1}^T)^T \\ &=\frac1NX^T(E_N-\frac1N\mathbb{I}_{N1}\mathbb{I}_{1N})(E_N-\frac1N\mathbb{I}_{N1}\mathbb{I}_{1N})^TX \\ &=\frac1NX^TH_NH_N^TX \\ &=\frac1NX^TH_NH_NX=\frac1NX^THX \end{aligned}$$

其中H称为中心矩阵，它的作用就是去中心化。容易验证H具有以下的良好性质

H^T = H Hⁿ = H

主成分分析中，我们的基本想法是将所有数据投影到一个子空间中，从而达到降维的目标，为了寻找这个子空间，我们基本想法是：

1. 所有数据在子空间中更为分散
2. 损失的信息最小，即：在补空间的分量少

原来的数据很有可能各个维度之间是相关的，于是我们希望找到一组p个新的线性无关的单位基u_i ,降 维就是取其中最重要的的q个基。于是对于一个样本x_i ,经过这个坐标变换后(方便说明先不减去平均值)： $$\hat{x_i}=\sum_{i=1}^p(u_i^Tx_i)u_i=\sum_{i=1}^q(u_i^Tx_i)u_i+\sum_{i=q+1}^p(u_i^Tx_i)u_i$$

我们选取方差最大的方向为我们的保留方向，不妨如下设定J

$$\begin{gathered} \text{J} =\frac1N\sum_{i=1}^N\sum_{j=1}^q((x_i-\overline{x})^Tu_j)^2 \\ =\sum_{j=1}^qu_j^TSu_j , s.t. u_j^Tu_j=1 \end{gathered}$$

由于每一个基都是线性无关的，我们可以分别求解每一个基，因此原问题变为一个优化问题

$$argmax_{u_j}L(u_j,\lambda)=argmax_{u_j}u_j^TSu_j+\lambda(1-u_j^Tu_j)\\\\\\Su_j=\lambda u_j$$

不难发现，我们需要的基就是协方差矩阵的本征矢(特征向量)，我们选取特征值最大的前q项即可。

等价方法：奇异值分解

对中心化后的数据集进行奇异值分解： HX = UΣV^T, U^TU = E_N, V^TV = E_p, Σ : N × p 于是： $$S=\frac1NX^THX=\frac1NX^TH^THX=\frac1NV\Sigma^T\Sigma V^T$$ 因此，我们直接对中心化后的数据集进行 SVD,就可以得到特征值和特征向量V ,在新坐标系中的坐标就是：

HX ⋅ V